Mouvement et interaction - Spécialité
Mouvement dans un champ uniforme
Exercice 1 : Chute libre d'une balle (Attention au signe lorsqu'on projette les équations
On jette une balle \( B \) dans un champ de pesanteur \(\vec{g}\) avec une vitesse \(\vec{v_0}\).
Faire le bilan des forces en écrivant la résultante \(\vec{F}\).On écrira \(\vec{F} = ... \)
On appelera \(a_y\) le projeté de \(\vec{a}\) sur l'axe \( y \).
On appelera \(v_y\) le projeté de la vitesse \(v_0\) sur l'axe \( y \) à l'instant \( 0 \).
On appelera \(h\) la distance du sol à laquelle la balle se trouve à l'instant \( 0 \).
Application numérique
Déterminer au bout de combien de temps la balle touche le sol.On donne :
- \(v_y = 5,0 km/h \)
- \(h = 1,2 m \)
- \(g = 9,807 m\mathord{\cdot}s^{-2} m.s^{-2} \)
Exercice 2 : Déterminer une vitesse grâce à l'énergie mécanique
Un enfant glisse le long d’un toboggan de plage dans le référentiel terrestre supposé galiléen.
Pour l’exercice, l’enfant sera assimilé à un point matériel \( G \) et on négligera tout type de frottement ainsi que toutes les actions dues à l’air.
Un toboggan de plage est constitué de :
- une piste \( DO \) qui permet à un enfant partant de \( D \), sans vitesse initiale, d’atteindre le point \( O \) avec une vitesse \( V_0 \).
- une piscine de réception : la surface de l’eau se trouve à une distance \( H \) au-dessous de \( O \).
- Masse de l’enfant : \( m = 29 kg \)
- Intensité de la pesanteur : \( g = 9,8 m\mathord{\cdot}s^{-2} \)
- Dénivellation \( h = 5,5 m \)
- Hauteur \( H = 0,5m \)
- On choisit l’altitude du point \( O \) comme référence pour l’énergie potentielle de pesanteur de l’enfant, \( E_{pO} = 0 \) pour \(y_0 = 0\).
Calculer l’énergie potentielle de pesanteur \( E_{pD} \) de l’enfant au point \( D \).
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Exercice 3 : Rappel de formules sur l'énergie et la vitesse
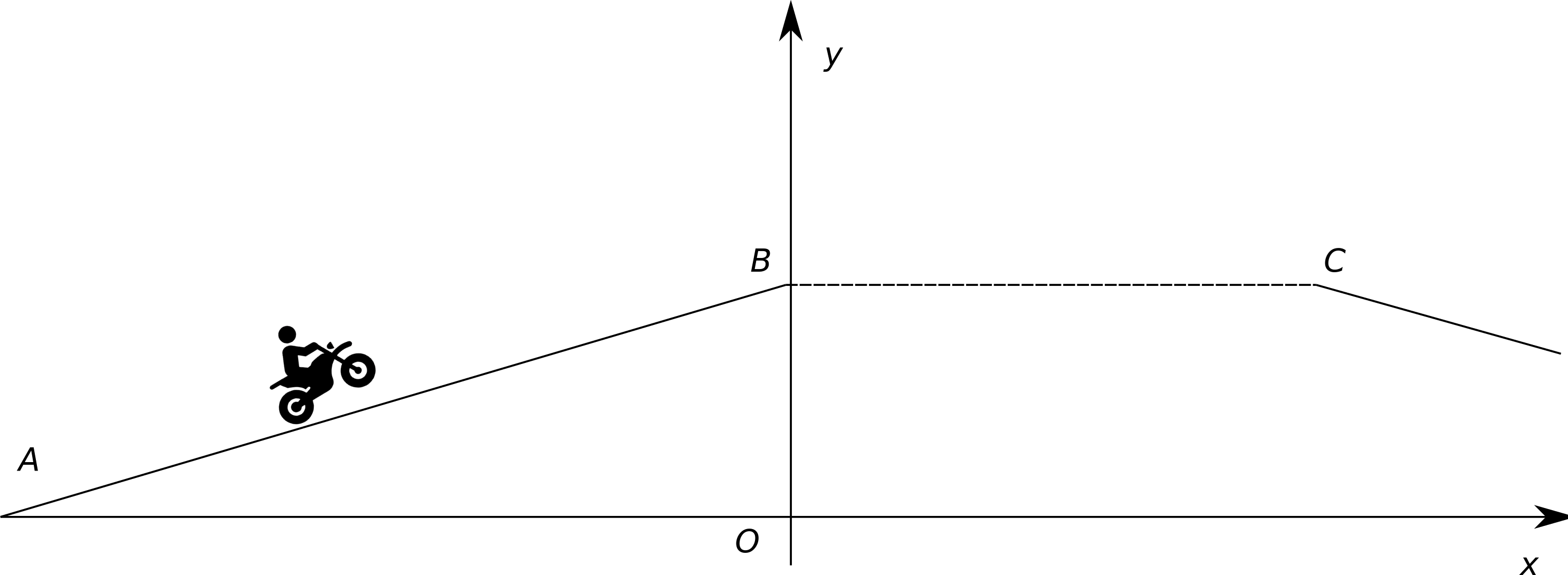
Un sportif intrépide tente de battre le record de saut en longueur à moto.
L’axe \( Ox \) est le niveau de référence des énergies potentielles de pesanteur.
- Intensité de la pesanteur : \( g = 9,8 m\mathord{\cdot}s^{-2} \)
- Masse du système : \( m = 160 kg \)
- \( AB = 57 m \)
Soit un tremplin incliné d’un angle \( \alpha = 29° \) par rapport à l'axe \( Ox \).
On considère que le motard parcourt le tremplin \( AB \) avec une vitesse de valeur constante égale à \( 221 km/h \).
Au point \( B \) il s'envole pour un saut d’une portée \( BC = 130 m \).
Entre \( B \) et \( C \), toute force autre que le poids est supposée négligeable.
On donnera un résultat avec 3 chiffres significatifs, en \( km / h \) et suivi de l'unité qui convient.
Exercice 4 : Problème sur l'énergie mécanique (jet de projectile)
Les balles en mousse sont des sphères de diamètre \(6\:cm\) et de masse \(68\:g\).
Données
- - Intensité du champ de pesanteur : \( g = 9,80665\:m\mathord{\cdot}s^{-2} \)
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
En supposant que l'énergie cinétique transmise aux balles est la même que dans l'expérience précédente, déterminer la nouvelle hauteur maximale à laquelle on peut envoyer les balles.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Déterminer la masse des nouveaux projectiles.
On donnera le résultat avec 2 chiffres significatifs et suivi de l'unité qui convient.
Exercice 5 : Obtenir la distance entre le filet et le point de chute d'un ballon après un service au volley-ball
Pour servir au volley-ball, un joueur lance un ballon et le frappe à une hauteur \( h = 3,2\:m \) au-dessus de la ligne de fond du terrain. On étudie la trajectoire du centre de masse \( G \) du ballon dans un référentiel terrestre considéré comme galiléen. L'étude du mouvement se fera dans le repère \( (O;\vec{i},\vec{j}) \) représenté ci-dessous sans tenir compte des forces de frottements. Le vecteur vitesse initial \( \vec{v_0} \) du ballon, dont l'origine est le point \( P(0 ; h) \), forme un angle \( \alpha = 4 \)° avec le vecteur \( \vec{i} \).
- - intensité du champ de pesanteur : \( g = 9,81\:m\mathord{\cdot}s^{-2} \);
- - \( \| \vec{v_0} \| = 23\:m\mathord{\cdot}s^{-1} \);
- - demi-longueur du terrain : \( D = 9\:m \);
- - hauteur du filet : \( H = 2,43\:m \);
- - rayon du ballon : \( R = 0,2\:m \).
Déterminer la distance depuis le filet jusqu'au point de chute du ballon.
On donnera le résultat en unités SI et avec 3 chiffres significatifs. On utilisera les valeurs exactes pour faire les calculs, et on arrondira au dernier moment.